Types Of Discontinuity
Discontinuity is a concept in mathematics that describes the behavior of a function at a particular point. A function is continuous if its graph can be drawn without lifting the pen from the paper. If there is a “hole” or a “jump” in the graph, the function is considered discontinuous. Understanding the different types of discontinuities is important in various fields of mathematics, such as calculus, algebra, and geometry.
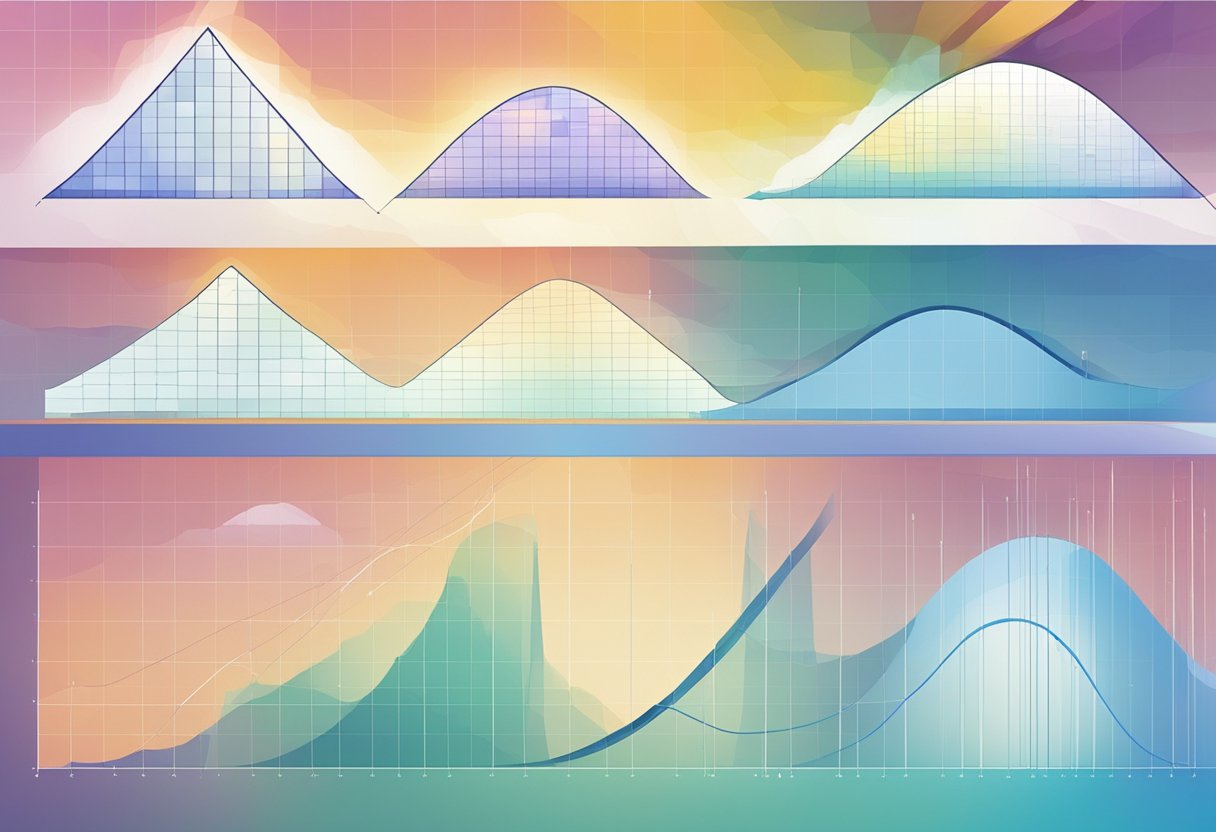
There are different types of discontinuities, including jump, infinite, removable, endpoint, and mixed. Jump discontinuities occur when the limit of the function from the left and right sides of the point is finite, but the function value at the point is different. Infinite discontinuities occur when the limit of the function from the left or right side of the point is infinite. Removable discontinuities occur when the limit from both sides of the point is finite and equal, but the function value at the point is undefined. Endpoint discontinuities occur at the endpoints of a function’s domain, where the limit from one side of the endpoint does not exist. Mixed discontinuities occur when a function has more than one type of discontinuity at a single point.
Key Takeaways
- Discontinuity is a concept in mathematics that describes the behavior of a function at a particular point.
- There are different types of discontinuities, including jump, infinite, removable, endpoint, and mixed.
- Understanding the different types of discontinuities is important in various fields of mathematics, such as calculus, algebra, and geometry.
Understanding Continuity and Discontinuity
Defining Continuity
In mathematics, a continuous function is a function that does not have any abrupt changes in its behavior. A function is continuous at a point if the limit of the function exists at that point and is equal to the function’s value at that point. In other words, a function is continuous at a point if it can be drawn without lifting the pen from the paper.
A continuous function is defined for all values in its domain, and its graph is a smooth curve without any breaks or jumps. A continuous function can be defined both algebraically and graphically, and it is a fundamental concept in calculus and analysis.
Defining Discontinuity
On the other hand, a discontinuous function is a function that has abrupt changes in its behavior. A function is discontinuous at a point if the limit of the function does not exist at that point or if it is not equal to the function’s value at that point. In other words, a function is discontinuous at a point if it cannot be drawn without lifting the pen from the paper.
Discontinuities can be classified into different types, such as jump, infinite, removable, endpoint, or mixed. A removable discontinuity is characterized by the fact that the limit exists, and it can be “fixed” by re-defining the function. The other types of discontinuities are characterized by the fact that the limit does not exist.
Understanding Limits
A limit is a fundamental concept in calculus and analysis that helps us understand the behavior of functions near a particular point. The limit of a function at a point is the value that the function approaches as the input approaches that point. A limit can either exist or not exist, depending on the behavior of the function near that point.
If the limit of a function exists at a point, it means that the function is well-behaved near that point, and it can be approximated by a simple function. However, if the limit does not exist, it means that the function is not well-behaved near that point, and it cannot be approximated by a simple function.
Understanding Points
A point is a fundamental concept in geometry and analysis that helps us understand the behavior of functions at a particular location. A point can either be defined or undefined, depending on the context of the problem.
In the context of functions, a point is defined if it has a well-defined value, and it is undefined if it does not have a well-defined value. For example, the point (0,0) is well-defined in the Cartesian plane, but it is undefined in the polar coordinate system.
Conclusion
In conclusion, continuity and discontinuity are fundamental concepts in mathematics that help us understand the behavior of functions near a particular point. A continuous function is a function that does not have any abrupt changes in its behavior, while a discontinuous function is a function that has abrupt changes in its behavior. Limits and points are also important concepts that help us understand the behavior of functions near a particular location.
Types of Discontinuities
Discontinuity in mathematics is a point at which a function fails to be continuous. There are three main types of discontinuities: removable, jump, and infinite discontinuities. Each of these has its own unique characteristics.
Removable Discontinuities
A removable discontinuity occurs when a function has a hole at a certain point. This means that the function is undefined at that point, but the limit exists. This type of discontinuity can be fixed by redefining the function at the point of the hole. In other words, the function can be made continuous by filling in the hole with the correct value.
Jump Discontinuities
A jump discontinuity occurs when a function has a sudden jump at a certain point. This means that the left and right limits of the function exist, but they are not equal. The function “jumps” from one value to another at the point of the jump. This type of discontinuity can be caused by a change in the behavior of the function or a change in the domain.
Infinite Discontinuities
An infinite discontinuity occurs when a function approaches infinity or negative infinity at a certain point. This means that the limit of the function does not exist at that point. This type of discontinuity can be caused by a vertical asymptote in the function.
In summary, the three types of discontinuities are removable, jump, and infinite discontinuities. Each type has its own unique characteristics, and they can be caused by different factors. Understanding the different types of discontinuities is important in calculus and other areas of mathematics.
Analyzing Discontinuities in Functions
Discontinuities are an important aspect of functions that can help in understanding the behavior of a function. A discontinuity occurs when a function is not continuous at a certain point or interval. In this section, we will discuss different types of discontinuities in functions.
Discontinuities in Rational Functions
A rational function is a function that can be expressed as a ratio of two polynomial functions. Discontinuities in rational functions occur when the denominator of the function is equal to zero. These points are called vertical asymptotes, and they indicate that the function is not defined at those points. It is important to note that not all points where the denominator is zero are discontinuities. If the numerator is also zero at that point, it is a removable discontinuity.
Discontinuities in Piecewise Functions
A piecewise function is a function that is defined by different rules on different intervals. Discontinuities in piecewise functions occur at the points where the different rules meet. These points are called break points, and they can be classified as either removable or non-removable discontinuities.
Discontinuities in Composite Functions
A composite function is a function that is made up of two or more functions. Discontinuities in composite functions can occur at the points where the individual functions have discontinuities. It is important to note that not all points where the individual functions have discontinuities are discontinuities in the composite function.
In conclusion, analyzing discontinuities in functions is an important aspect of understanding the behavior of a function. Discontinuities can occur in rational functions, piecewise functions, and composite functions, and they can be classified as removable or non-removable. It is important to identify these points and understand their significance in order to fully understand the behavior of a function.
Mathematical Theorems and Discontinuity
Intermediate Value Theorem
The Intermediate Value Theorem is a theorem in calculus that states that if a continuous function takes on two values at two points in its domain, then it must also take on all values between those two points. This theorem is useful in determining whether a function has a root, or a point where the function equals zero, between two given points.
The Intermediate Value Theorem is closely related to the concept of continuity. If a function is continuous on an interval, then it must take on all values between its endpoints. Conversely, if a function takes on all values between two points, then it must be continuous on the interval between those points.
Theorems Defining Continuity at a Point
There are several theorems that define continuity at a point. One such theorem states that a function is continuous at a point if and only if the limit of the function at that point exists and is equal to the value of the function at that point.
Another theorem states that a function is continuous at a point if and only if the left-hand limit and the right-hand limit of the function at that point both exist and are equal to the value of the function at that point.
These theorems provide conditions for a function to be continuous at a point. If a function fails to meet these conditions, then it is discontinuous at that point.
The concept of continuity is closely related to the real numbers. A function is continuous on an interval if and only if it is continuous at every point in that interval. This means that the function must be defined and continuous for all real numbers in that interval.
Practical Implications of Discontinuity
Graphical Representation of Discontinuities
Discontinuities can be easily identified on a graph as breaks or gaps in the function. A graph of a continuous function will be a smooth curve with no breaks or gaps. On the other hand, a graph of a discontinuous function will have one or more breaks or gaps. Discontinuities can be classified into different types based on the nature of the break or gap.
Implications in Real-World Analysis
Discontinuities have practical implications in real-world analysis, particularly in areas such as finance, engineering, and physics. In finance, for example, discontinuities in stock prices can have significant implications for investment decisions. Similarly, in engineering, discontinuities in the behavior of a material can affect the design of structures and machines.
Discontinuities can also have implications in physics, particularly in the study of quantum mechanics. In quantum mechanics, the behavior of particles can be discontinuous, which can lead to phenomena such as quantum tunneling and quantum entanglement.
In addition, discontinuities can have implications in data analysis. Discontinuities in data can indicate errors or anomalies in the data, which can affect the accuracy of statistical analyses and predictions. Therefore, it is important to identify and understand the nature of discontinuities in data before conducting any analysis.
Overall, discontinuities can have significant practical implications in various fields, and it is important to understand their nature and effects.